Decision tree
·
A decision tree
is a tree-based supervised learning method used to predict the output of a
target variable.
·
Supervised
learning uses labeled data (data with known output variables) to make
predictions with the help of regression and classification algorithms.
·
Supervised
learning algorithms act as a supervisor for training a model with a defined
output variable.
·
It learns from
simple decision rules using the various data features.
· Decision trees in Python can be used to solve both classification and regression problems—they are frequently used in determining odds.
Useful Concepts
The decision tree algorithm breaks down a dataset into smaller subsets; while during the same time, an associated decision tree is incrementally developed. A decision tree consists of nodes (that test for the value of a certain attribute), edges/branch (that correspond to the outcome of a test and connect to the next node or leaf) & leaf nodes (the terminal nodes that predict the outcome) that makes it a complete structure.
An
example of a decision tree can be explained using above
binary tree. Let’s say you want to predict whether a person is fit given their information like age, eating
habit, and physical
activity, etc. The
decision nodes here are questions like ‘What’s the age?’, ‘Does he exercise?’,
and ‘Does he eat a lot of pizzas’? And the leaves, which are outcomes like
either ‘fit’, or ‘unfit’. In this case this was a binary classification problem
(a yes no type problem). There are two main types of Decision Trees:
1. Classification trees (Yes/No
types)
A
classification tree is an algorithm where the target variable is fixed or
categorical. The algorithm is then used to identify the “class” within which a
target variable would most likely fall.
An
example of a classification-type problem would be determining who will or will
not subscribe to a digital platform; or who will or will not graduate from high
school.
These
are examples of simple binary classifications where the categorical dependent
variable can assume only one of two, mutually exclusive values. In other cases,
you might have to predict among a number of different variables. For instance,
you may have to predict which type of smartphone a consumer may decide to
purchase.
In
such cases, there are multiple values for the categorical dependent variable.
Here’s what a classic classification tree looks like
1. Regression trees (Continuous
data types)
A
regression tree refers to an algorithm where the target variable is and the
algorithm is used to predict it’s value. As an example of a regression type
problem, you may want to predict the selling prices of a residential house,
which is a continuous dependent variable.
This will depend on both continuous factors like square footage as well as categorical factors like the style of home, area in which the property is located and so on.
Important
Terms Used in Decision Trees
1. Entropy:
Entropy is the measure of uncertainty or randomness in a data set. Entropy
handles how a decision tree splits the data.
It is calculated using
the following formula:
2. Information
Gain: The information gain measures
the decrease in entropy after the data set is split.
It is calculated as
follows:
IG(
Y, X) = Entropy (Y) - Entropy ( Y | X)
3. Gini
Index: The Gini Index is used to
determine the correct variable for splitting nodes. It measures how often a
randomly chosen variable would be incorrectly identified.
4. Root
Node: The root node is always the
top node of a decision tree. It represents the entire population or data
sample, and it can be further divided into different sets.
5. Decision
Node: Decision nodes are sub-nodes
that can be split into different sub-nodes; they contain at least two branches.
6. Leaf
Node: A leaf node in a decision tree
carries the final results. These nodes, which are also known as terminal nodes,
cannot be split any further.
How to avoid/counter Overfitting in
Decision Trees?
The common problem with
Decision trees, especially having a table full of columns, they fit a lot.
Sometimes it looks like the tree memorized the training data set. If there is
no limit set on a decision tree, it will give you 100% accuracy on the training
data set because in the worse case it will end up making 1 leaf for each
observation. Thus this affects the accuracy when predicting samples that are
not part of the training set.
Here are two ways to
remove overfitting:
1. Pruning Decision Trees.
2. Random Forest
Pruning
Decision Trees:
The splitting process
results in fully grown trees until the stopping criteria are reached. But, the
fully grown tree is likely to overfit the data, leading to poor accuracy on
unseen data.
In pruning, you trim
off the branches of the tree, i.e., remove the decision nodes starting from the
leaf node such that the overall accuracy is not disturbed. This is done by
segregating the actual training set into two sets: training data set, D and
validation data set, V. Prepare the decision tree using the segregated training
data set, D. Then continue trimming the tree accordingly to optimize the
accuracy of the validation data set, V.
In the above diagram,
the ‘Age’ attribute in the left-hand side of the tree has been pruned as it has
more importance on the right-hand side of the tree, hence removing overfitting.
Random
Forest:
Random Forest is an example of ensemble learning, in which we combine multiple machine learning algorithms to obtain better predictive performance.
While implementing the
decision tree we will go through the following two phases:
1. Building Phase
• Preprocess the dataset.
• Split the dataset from train and test
using Python sklearn package.
• Train the classifier.
2. Operational Phase
• Make predictions.
• Calculate the accuracy.
ID3:
There are many algorithms out there which construct Decision Trees, but one of the best is called as ID3 Algorithm. ID3 Stands for Iterative Dichotomiser 3. Before discussing the ID3 algorithm, we’ll go through few definitions. Entropy Entropy, also called as Shannon Entropy is denoted by H(S) for a finite set S, is the measure of the amount of uncertainty or randomness in data.
Intuitively,
it tells us about the predictability of a certain event. Example, consider a
coin toss whose probability of heads is 0.5 and probability of tails is 0.5.
Here the entropy is the highest possible, since there’s no way of determining
what the outcome might be. Alternatively, consider a coin which has heads on
both the sides, the entropy of such an event can be predicted perfectly since
we know beforehand that it’ll always be heads. In other words, this event has no
randomness hence it’s entropy is zero. In particular, lower values imply less uncertainty while higher values imply high uncertainty. Information Gain Information gain is also called as
Kullback-Leibler divergence denoted by IG(S,A) for a set S is the effective
change in entropy after deciding on a particular attribute A. It measures the
relative change in entropy with respect to the independent variables
IG(S, A) = H (S )- H (S, A)
Alternatively,
|
n |
IG(S, A) = H (S )- å P(x)* H (x)
i=0
where
IG(S, A) is the information gain by applying feature A. H(S) is the Entropy of
the entire set, while the second term calculates the Entropy after applying the
feature A, where P(x) is the probability of event x. Let’s understand this with
the help of an example Consider a piece of data collected over the course of 14
days where the features are Outlook, Temperature, Humidity, Wind and the
outcome variable is whether Golf was played on the day. Now, our job is to
build a predictive model which takes in above 4 parameters and predicts whether
Golf will be played on the day. We’ll build a decision tree to do that using ID3 algorithm.
|
Day |
Outlook |
Temperature |
Humidity |
Wind |
Play Golf |
|
D1 |
Sunny |
Hot |
High |
Weak |
No |
|
D2 |
Sunny |
Hot |
High |
Strong |
No |
|
D3 |
Overcast |
Hot |
High |
Weak |
Yes |
|
D4 |
Rain |
Mild |
High |
Weak |
Yes |
|
D5 |
Rain |
Cool |
Normal |
Weak |
Yes |
|
D6 |
Rain |
Cool |
Normal |
Strong |
No |
|
D7 |
Overcast |
Cool |
Normal |
Strong |
Yes |
|
D8 |
Sunny |
Mild |
High |
Weak |
No |
|
D9 |
Sunny |
Cool |
Normal |
Weak |
Yes |
|
D10 |
Rain |
Mild |
Normal |
Weak |
Yes |
|
D11 |
Sunny |
Mild |
Normal |
Strong |
Yes |
|
D12 |
Overcast |
Mild |
High |
Strong |
Yes |
|
D13 |
Overcast |
Hot |
Normal |
Weak |
Yes |
|
D14 |
Rain |
Mild |
High |
Strong |
No |





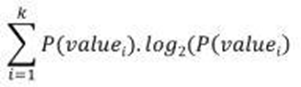



0 Comments